Urban combat theaters and disaster scenarios present a unique challenge as personnel must move rapidly to forward positions while transporting heavy mission-critical equipment up and down stairs. These environments are inherently unstructured, which currently limits the use of robots in these missions. This project aims to identify what technology gaps exist to carry heavy payloads upstairs in unstructured environments quickly. We will accomplish the project goal by defining metrics for robot comparison, establishing the current state-of-the-art baselines, designing and building novel propulsive mechanisms, experimentation and design iteration, integrating multimodal sensing, and developing autonomous control.
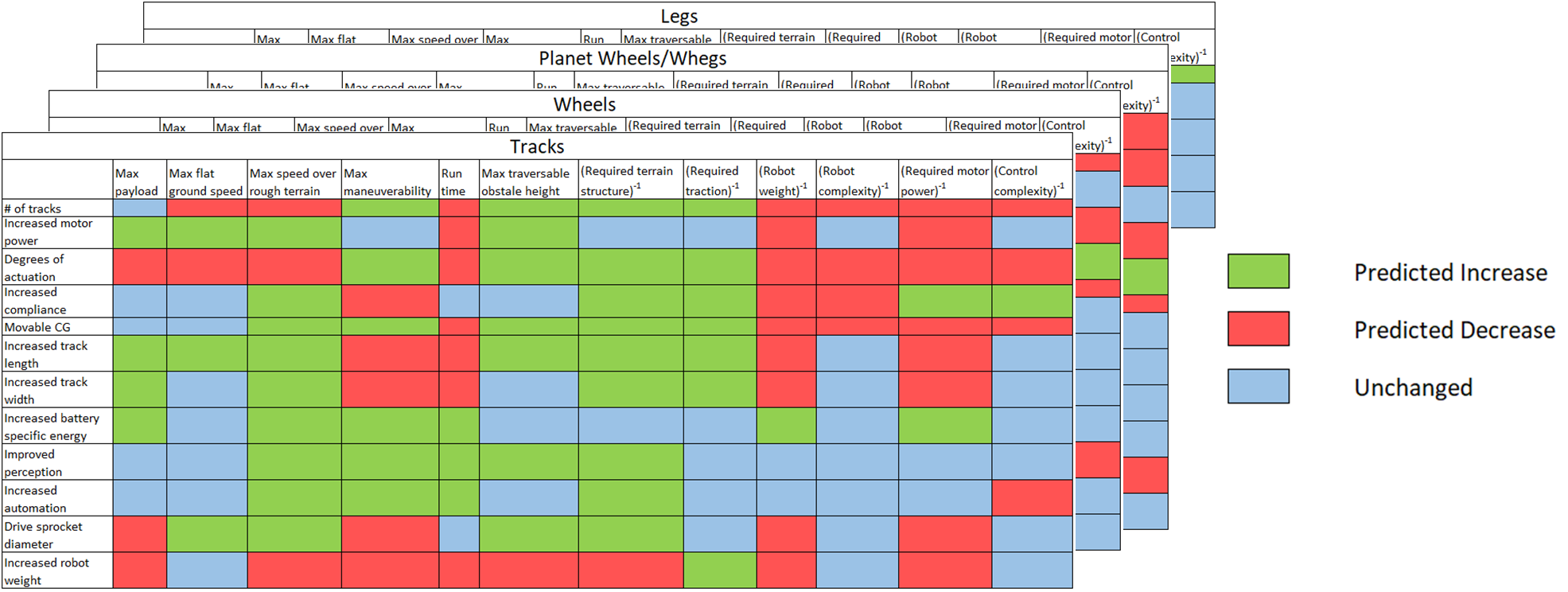
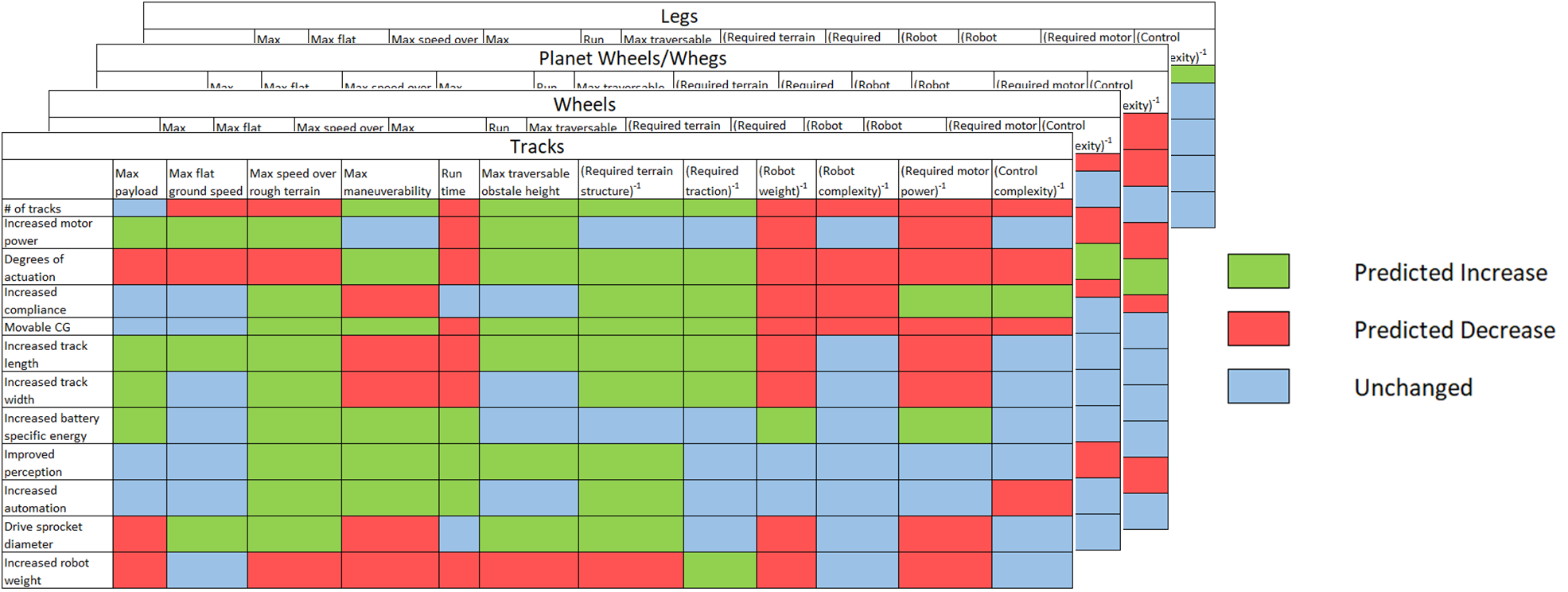While working towards the project goal, we will develop design gradients to better understand the proposed capabilities range and tradeoffs among them. For example, if we add more powerful motors, then intuitively, we would expect the robot payload to increase, but the relationship, in reality, would not be linear. Increasing motor power increased motor weight and required battery power, increasing the overall robot weight, which might reduce the payload capability. By utilizing the design gradients, we ensure that the design decisions made throughout the project will result in better-performing robots. Each robot iteration will further refine our design gradients, effectively creating a feedback loop that will ultimately lead to accomplishing the project goals.
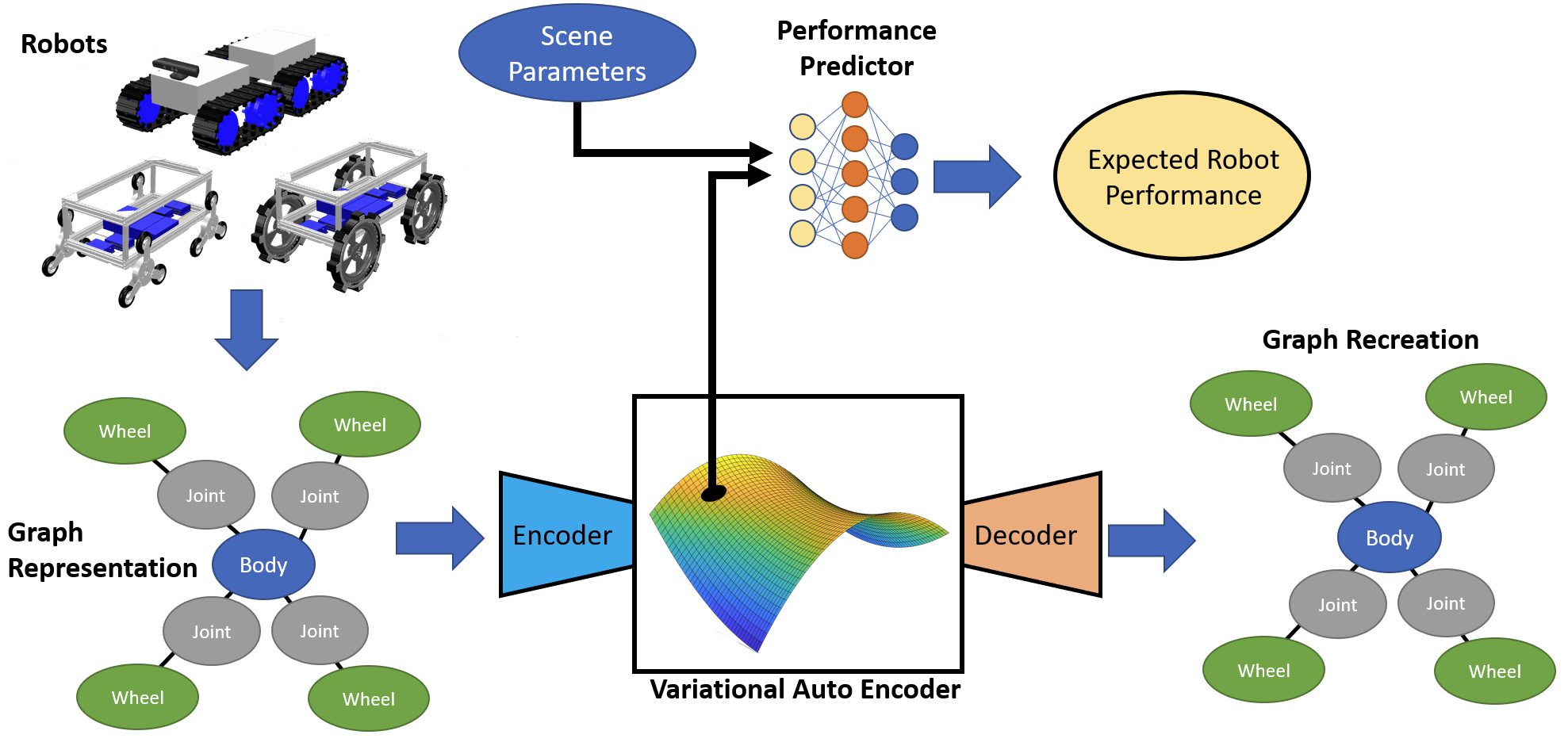
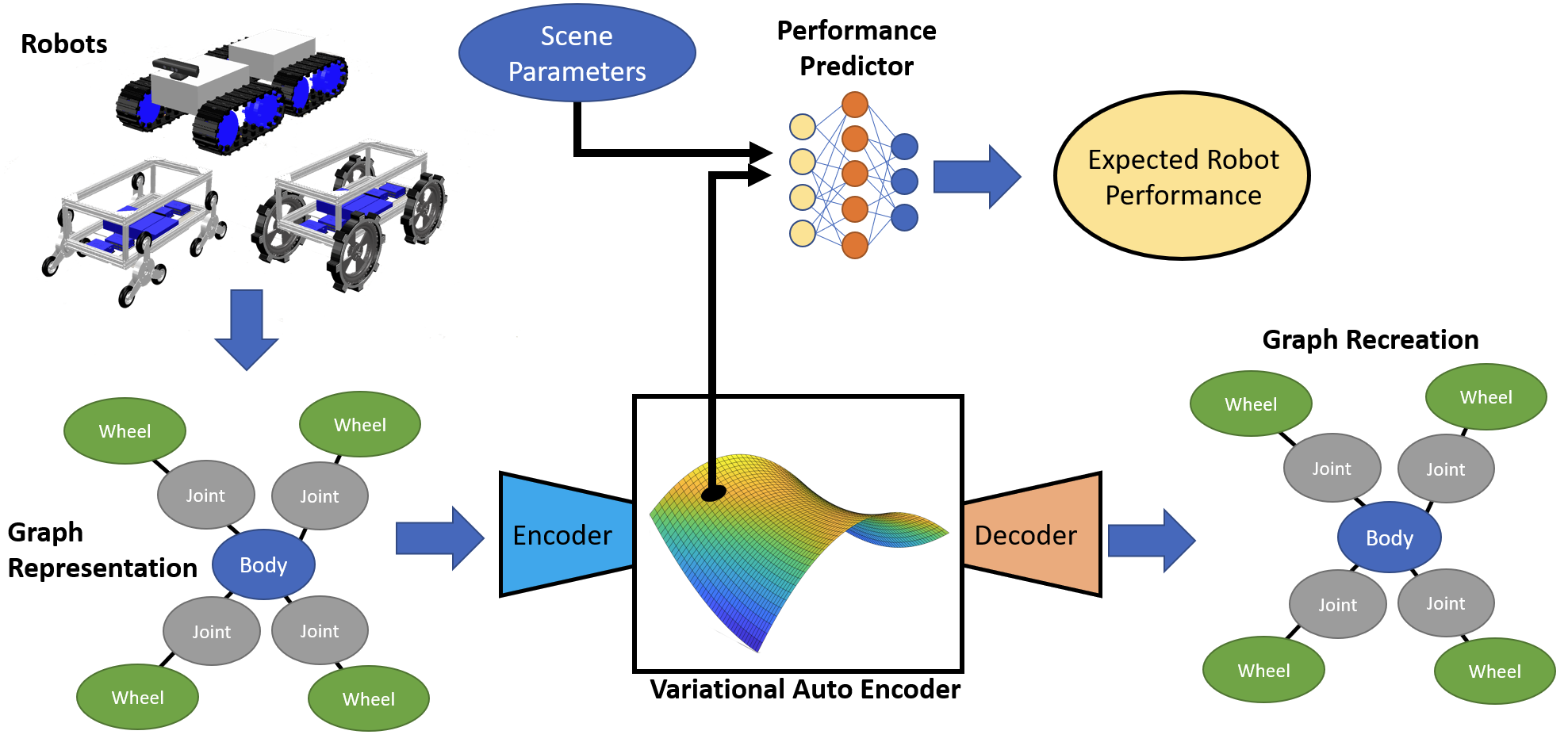The design gradients mentioned above are analogous to first-order approximations calculated by perturbing a particular robot parameter and measuring the change in performance, which is limited to comparisons within a specific propulsive mechanism group. For example, if we increase the wheelbase on a tracked robot, the climbing speed will increase, but that may not be true for a wheeled robot. We hypothesize that if we can encode robots of various morphologies onto a common continuous latent space, then on that latent space, we can calculate design gradients that are not unique to one particular morphology. To accomplish this, first, we will create a graph representation of a specific robot. Then we will encode the graph representation onto the latent space using a message-passing neural network coupled with a graph variational autoencoder. The robot’s latent space representation will be input into a performance-predicting neural network (PPN) and a decoder. We will utilize the PPN to calculate the expected performance of the robot and the decoder to estimate the original graph representation. By training the encoder and PNN end-to-end, we force robots with similar abilities to be clustered together on the latent space, even if the robot morphologies are very different. Once training is complete, we can encode a robot onto the latent space, perturb that latent space location and calculate the change in performance with the PNN. This difference in performance over the change in latent space location enables us to calculate the design gradients. We will use the design gradients to identify a performance maximum on latent space and decode the maximum to obtain an optimized robot morphology.
