With the rapid development of affordable robots with embedded sensing and computation capabilities, we are quickly approaching a point at which real-life applications will involve the deployment of hundreds, if not thousands, of robots. Most existing algorithms can be categorized as coupled approaches, which search the full configuration space of a system, and decoupled approaches, which search some low-dimensional representation. Coupled approaches can be guaranteed to find an optimal path, but are computationally infeasible for large numbers of robots. In other words, these approaches suffer from the curse of dimensionality, which states that the size of a system’s configuration space grows exponentially with the dimensionality of the system. Decoupled approaches scale better with the number of robots, but cannot generally be guaranteed to find a path. Most prior works give us a choice: scalability or guarantees, but not both.
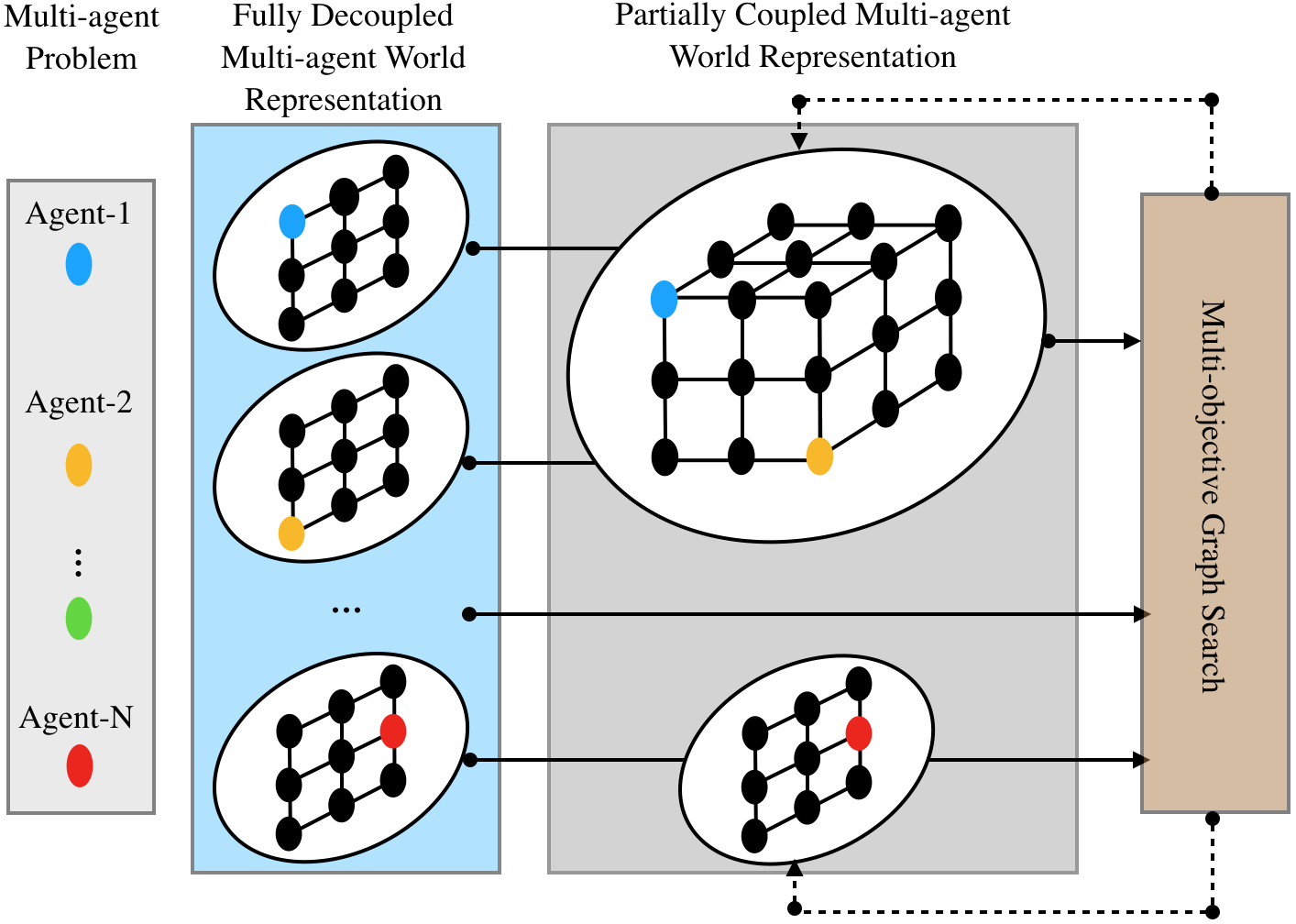
We seek to obtain the benefits of both coupled and decoupled approaches: we made the observation that in multi-agent planning, not all agents come into close proximity to each other and therefore do not require a coordinated planner. These agents can simply rely on a computationally efficient single agent planner, until they come into close proximity to each other, at which point the agents nearby to each other must use a coordinated planner among themselves. The idea here is that if agents only coordinate when needed, then the curse of dimensionality may not be realized, but in actuality, in the worst case it will. We call this dynamic coupling of agents, as needed, subdimensional expansion,
Subdimensional expansion is not a planner but rather an adaptation of existing planners, such as A* and RRTs. This approach first generates an individually (sometimes optimal) plan for each agent, ignoring the other agents. For an N-agent system, the initial search yields N paths, which essentially is a one-dimensional subset of the NM-dimensional configuration space where M is the number of degrees of freedom each agent has. Subdimensional expansion that directs the robots to follow these paths until the goal is reach or an agent-agent collision is detected. At the collision, the search space is then locally increased in dimensionality along any path found by the planning algorithm leading to the collision. Such a space grows, as needed, to determine the (optimal) path to the goal. Doing so constructs a variable dimensional search space of minimal size which will contain the optimal path.
We implemented subdimensional expansion for the case where the configuration space of each robot can be represented as a graph, using A* as the underlying path planning algorithm. We name the resulting algorithm M*. M* can be proven to find an optimal path in finite time, or to terminate in finite time that no path exists.
Starting from the subdimensional expansion and the conventional (standard) multi-agent path finding (MAPF) problem, we investigated other variants of MAPF problems while exploiting the dynamic-coupled planning strategy. Conventional multi-agent path planners typically aim to plan an ensemble of paths that optimizes a single objective, such as path length. Many applications, however, may require multiple objectives, say time-to-completion, fuel use and path risk, to be simultaneously optimized in the planning process. Often, these criteria may not be directly compared and sometimes lie in competition with each other. Simply applying standard multi-objective search algorithms to multi-agent path finding may prove to be inefficient because the size of the space of possible solutions, i.e., the Pareto-optimal set, can grow exponentially with the number of agents. We therefore formulated the problem called multi-objective multi-agent path finding (MOMAPF) and developed planners, such as multi-objective M* (MOM*), multi-objective conflict-based search (MO-CBS), to solve the problem, which leverage both dynamic-coupled planning strategy for MAPF and dominance principles from the multi-objective optimization literature. Consequently, the developed planners are able to compute the entire Pareto-optimal front while search efficiently by constructing a variable dimensional search space.
Another important variant of MAPF we considered is to let a team of agents collectively visit a large number of goal locations (also called waypoints) before reaching their destinations. We call this problem multi-agent simultaneous multi-goal sequencing and path finding (MSMP) and this problem manifests itself in applications ranging from surveillance to logistics. MSMP involves not only planning collision-free paths but also sequencing multiple goal locations, i.e. assigning goals to agents as well as specifying the visiting order of goals. Solving MSMP is challenging and most of the existing methods consider only a limited aspect of the problem. On one hand, multiple travelling salesman (mTSP) probl
